Indholdsfortegnelse:

Video: Hvordan implementerer du et binært søgetræ i Java?

2024 Forfatter: Lynn Donovan | [email protected]. Sidst ændret: 2023-12-15 23:45
Implementering af et binært søgetræ (BST) i Java
- Det venstre undertræ af en node indeholder kun noder med nøgler mindre end nodens nøgle.
- Det højre undertræ af en node indeholder kun noder med nøgler, der er større end nodens nøgle.
- Det venstre og højre undertræ skal hver også være en binært søgetræ .
- Der må ikke være duplikerede noder.
Spørgsmålet er også, hvordan implementeres binær søgning i Java?
Lad os se et eksempel på binær søgning i java, hvor vi skal søge et element fra et array ved hjælp af rekursion
- klasse BinarySearchExample1{
- public static int binarySearch(int arr, int first, int last, int key){
- if (sidste>=første){
- int mid = første + (sidste - første)/2;
- if (arr[mid] == tast){
- returnere midt;
- }
For det andet, hvor bruger vi binært søgetræ? Binært søgetræ - Brugt i mange Søg applikationer, hvor der hele tiden kommer data ind/ud, såsom kortet og sæt objekter i mange sprogs biblioteker. Binær Space Partition - Brugt i næsten alle 3D-videospil for at bestemme, hvilke objekter der skal gengives.
Bare så, hvordan dannes binære træer?
Oprettelse af binært træ ved hjælp af rekursion
- Læs en data i x.
- Tildel hukommelse til en ny node og gem adressen i markøren s.
- Gem data x i noden p.
- Opret rekursivt det venstre undertræ af p og gør det til venstre underordnet af p.
- Opret rekursivt det rigtige undertræ af p og gør det til det rigtige underordnede af p.
Hvad er kompleksiteten af binær søgning?
Binær søgning løber ind på det værste logaritmiske tidspunkt og laver O(log n) sammenligninger, hvor n er antallet af elementer i arrayet, O er Big O notationen, og log er logaritmen. Binær søgning tager konstant (O(1)) plads, hvilket betyder, at pladsen optaget af algoritmen er den samme for et hvilket som helst antal elementer i arrayet.
Anbefalede:
Hvordan implementerer du set interface i Java?
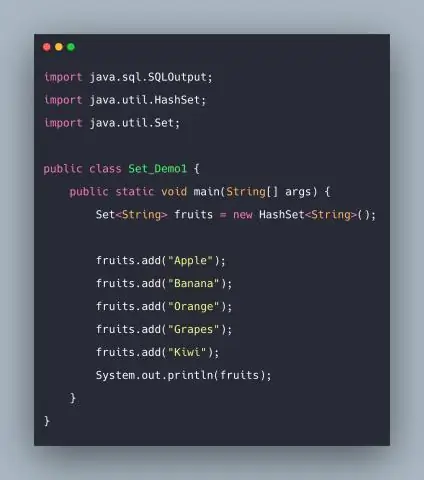
Set in Java Set er en grænseflade, der udvider Collection. Det er en uordnet samling af objekter, hvor duplikerede værdier ikke kan gemmes. Grundlæggende er Set implementeret af HashSet, LinkedHashSet eller TreeSet (sorteret repræsentation). Set har forskellige metoder til at tilføje, fjerne clear, størrelse osv. for at forbedre brugen af denne grænseflade
Hvad er worst case og gennemsnitlige sagskompleksitet for binært søgetræ?

Binært søgetræ Algoritme Gennemsnit Værste tilfælde Mellemrum O(n) O(n) Søg O(log n) O(n) Indsæt O(log n) O(n) Slet O(log n) O(n)
Hvordan lagres lyddata binært?

Bits er simpelthen binær information (nuller og enere), der danner dataene, som gemmer musikken. Bitdybden fortæller dig antallet af bits, der bruges til at lagre lydsignalet. Processen med at gemme musik i et digitalt format involverer udskæring af lydsignalet og lagring af hvert udsnit som en binær kode
Hvordan håndterer du binært overløb?

Overløbsregel for addition Hvis 2 To's komplementtal tilføjes, og de begge har samme fortegn (begge positive eller begge negative), så opstår overløb, hvis og kun hvis resultatet har det modsatte fortegn. Overløb opstår aldrig, når der tilføjes operander med forskellige fortegn
Hvordan implementerer du en abstrakt klasse i Java?

Hvis en klasse erklæres abstrakt, kan den ikke instansieres. For at bruge en abstrakt klasse, skal du arve den fra en anden klasse, levere implementeringer til de abstrakte metoder i den. Hvis du arver en abstrakt klasse, skal du levere implementeringer til alle de abstrakte metoder i den
