
Video: Hvad betyder Injektiv?
2024 Forfatter: Lynn Donovan | [email protected]. Sidst ændret: 2023-12-15 23:45
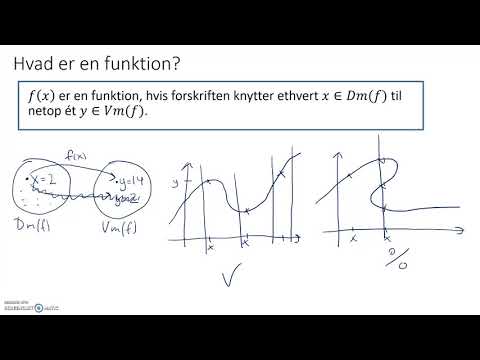
I matematik, en injektiv funktion (også kendt som injektion eller en-til-en-funktion) er en funktion, der kortlægger distinkte elementer af sit domæne til distinkte elementer i sit codomæne. Med andre ord er hvert element i funktionens codomæne billedet af højst ét element af dets domæne.
På samme måde kan du spørge, hvad er et eksempel på en injektiv funktion?
Eksempel : Det fungere f(x) = x2fra mængden af positive reelle tal til positive reelle tal er begge dele injektiv og surjektiv. Sådan er det også bijektiv . Men det samme fungere fra sættet af alle reelle tal er det ikke bijektiv fordi vi kunne have, for eksempel , begge.
Derudover, hvordan beviser du Surjektiv og Injektiv? da f er en bijektion. Til bevise en funktion er objektiv, skal du bevise at det er injektiv og også surjektiv . " Injektiv " betyder, at ikke to elementer i funktionens domæne bliver mappet til det samme billede." Surjektiv " betyder, at ethvert element i funktionens område rammes af funktionen.
Er den tomme funktion derfor injektiv?
Ifølge denne definition kan evt tom funktion er ikke injektiv fordi ˘f:S→∅ ikke er en fungere.
Hvordan ved man, om en funktion er grafisk?
For en-en: bare tegn lodrette linjer (vinkelret på x-aksen), så hvis du finder en lodret linje, der skærer kurven af fungere så er det ikke en-en. Hvad angår en-en, bør enhver lodret linje skære kurve af fungere på et tidspunkt!
Anbefalede:
Hvad betyder S på Instax Mini 9?

På bagsiden vil du bemærke, at filmtællerdisplayet (antallet af resterende optagelser) er indstillet til S. Dette skyldes, at du stadig skal skubbe det sorte filmdæksel ud. For at gøre dette skal du blot tænde kameraet ved at trykke på den store knap placeret direkte ved siden af objektivet og trykke på udløserknappen
Hvad betyder set i SAS?

SET læser en observation fra et eksisterende SAS-datasæt. INPUT læser rådata fra en ekstern fil eller fra in-stream datalinjer for at skabe SAS-variabler og observationer. Brug af indstillingen KEY= med SET giver dig adgang til observationer non-sekventielt i et SAS-datasæt i henhold til en værdi
Hvad betyder CLS i batch-fil?

Type: Kommando
Hvad betyder hvis betyder i pseudokode?
'Udvælgelsen' er 'hvis så andet'-udsagnet, og iterationen opfyldes af en række udsagn, såsom 'mens', 'gør' og 'for', mens sagstype-sætningen opfyldes af 'switch'-erklæringen. Pseudokode er et kunstigt og uformelt sprog, der hjælper programmører med at udvikle algoritmer
Hvad betyder case, når betyder i SQL?

SQL CASE-sætningen CASE-sætningen gennemgår betingelser og returnerer en værdi, når den første betingelse er opfyldt (som en IF-THEN-ELSE-sætning). Så når en betingelse er sand, stopper den med at læse og returnerer resultatet. Hvis ingen betingelser er sande, returnerer den værdien i ELSE-sætningen
