
Video: Hvad er det for et polynomium?

2024 Forfatter: Lynn Donovan | [email protected]. Sidst ændret: 2023-12-15 23:45
Typer af Polynomier er Monomial, Binomial, Trinomial. Monomial er polynomium med et led er Binomial polynomium med to ulige udtryk, og Trinomial er polynomium med tre, i modsætning til udtryk. Lad os studere om alle tre typer Polynomier en efter en.
I betragtning af dette, hvad er polynomier med eksempler?
Eksempler på polynomier
| Eksempel polynomium | Forklaring |
|---|---|
| 5x +1 | Da alle variablerne har heltalseksponenter, der er positive, er dette et polynomium. |
| (x7 + 2x4 - 5) * 3x | Da alle variablerne har heltalseksponenter, der er positive, er dette et polynomium. |
| 5x-2 +1 | Ikke et polynomium, fordi et led har en negativ eksponent |
Efterfølgende er spørgsmålet, er 34 et polynomium? Et monomial er en polynomium med kun et led, såsom 3x, 4xy, 7 og 3x2y 34 . Et binomial er en polynomium med præcis to led, såsom x + 3, 4x2 + 5x og x + 2y7. Et trinomium er en polynomium med præcis tre led, såsom 4x4 + 3x3 – 2.
hvilken slags polynomium har 4 led?
Man kan sige, at det er et kvadrinomium, men det betyder bare, at det har 4 led. Hvis disse udtryk er i en enkelt variabel af højeste grad 3, så hedder det en kubik.
Hvad er et polynomium med 5 led?
Svar: 1) Monomial 2) Trinomial 3) Binomial 4) Monomial 5 ) Polynomium . 2. Grad.
Anbefalede:
Hvad kalder man et polynomium med 6 led?
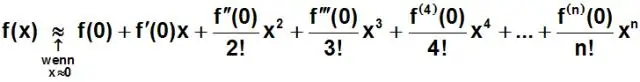
Følgende navne tildeles polynomier i overensstemmelse med deres grad: Grad 4 – kvarts (eller, hvis alle led har lige grad, bikvadratisk) Grad 5 – kvintisk. Grad 6 - sextisk (eller, mindre almindeligt, heksisk)
Hvad er 3. grads polynomium?

Tredjegradspolynomier er også kendt som kubiske polynomier. Cubics har disse egenskaber: En til tre rødder. To eller nul ekstremer. Rødder kan løses af radikaler
Er Pi et polynomium?

Pi (π) betragtes ikke som et polynomium. Det er en værdi, der refererer til en cirkels omkreds. På den anden side refererer polynomium til en ligning, der indeholder fire variable eller flere
Hvad er et ækvivalent polynomium?

Derudover er to polynomier ækvivalente, hvis alle koefficienterne for den ene er et konstant (ikke nul) multiplum af de tilsvarende koefficienter for den anden
Er summen af to polynomier altid et polynomium?

Summen af to polynomier er altid et polynomium, så forskellen mellem to polynomier er også altid et polynomium
